Travel Hunch: How long will it take to drive from your house to a relative’s house 300 miles away?
The obvious thought is that most highway speed limits are 55 mph to 65 mph and, given an average speed of 60 mph, 300 miles will take roughly five hours of driving time. Roughly. Five hours is simply an estimate, and the use of the term ‘roughly’ implies that it is not exact; that there is some window of time around the 5-hour estimate. That window is what we vaguely recognize as uncertainty. But how big is that window? Do you care if you arrive 4 hours and 55 minutes from the time you leave instead of the 5 hours you thought it would take? Does it matter if you’re there 5 minutes later than expected? Hmmm . . . expected is another good word to remember. You have an expected time of arrival, based on your rough estimate, and then some window of variation, or uncertainty, around that expected arrival time. So, if you’re just going to visit for the weekend, then it probably doesn’t matter if you’re as much as an hour early or late. But if you need to be there for a holiday dinner that will be served at a specific time, then it’s probably more important to arrive early than to be late, right? Just how early could you be though? Could you get there in 4-1/2 hours? 4 hours? 3 hours? There are speed limits and safety to consider, so you’re probably not going to make it any sooner than 300 miles ÷ 70 mph = 4.3 hours, or 4 hours and 15 minutes. However, if you’re the type that likes to get out and stretch every so often or stop for coffee or a bite to eat, then it could easily take you much longer than the estimated 5 hours to get there. These ‘factors’ cause the actual arrival time to vary from the estimated arrival time. Depending on how much detail you want to consider, you could determine, within a few seconds, exactly when you will arrive. But then there are the unknowns. You don’t plan to get stuck behind an accident that slows you down. You don’t expect to hit a deer on the highway, have a flat tire, or otherwise get delayed. How would you build those factors, or uncertainty components, into the equation? Exacting as you might want to be, you simply can’t always predict all the uncertainty components that could cause you to deviate from your precise estimate of arrival time. But you can build in ‘fudge factors’ to account for them. Using your best educated guess, you can put a time estimate on each variable that you could possibly encounter in traveling from your house to your destination. Combine these uncertainty components, and you get a total uncertainty, or time window, to place around your initial estimate of arrival time.
Cookie Munch: Why don’t your cookies turn out like Mom’s when you both use the same recipe?
The variables, or uncertainty components, that cause a discernable difference between your cookies and your mother’s might include: brand of the ingredients your mother uses vs. the brands you use, measuring differences (does she use something to measure each ingredient, or is it just a ‘pinch’?), baking temperature, altitude, etc. Changing one or two of these only slightly may not make a noticeable difference, but little changes to many of them could make all the difference. Add up all those variances and you get a large enough uncertainty to make the resulting cookies have a different taste, texture, color, etc. You could place upper and lower limits on each of these variables to make sure you get a more consistent result for the cookies you make. You might change the recipe to state that you should use no more than or no less than X amount of Brand A sugar, within 10% of what is called out in the recipe; use Y amount of Brand B flour ±10%; and use a specific size package of Brand C chocolate chips, not to deviate more than 1 oz. You could also specify the baking temperature and/or the baking time, based on the altitude and give a different temperature or baking time for different altitudes so that someone living in the Mile-High City of Denver can achieve the same result as someone living in a coastal town. Locking down the variables produces a more consistent result, and that is a good way to control quality! How much you lock these down depends upon your ability to measure accurately as well as each variable’s sensitivity factor. A sensitivity factor can be determined by experimenting. How much can you change the amount of sugar in the recipe before you can taste (or see) a difference? The sugar probably has a smaller sensitivity factor than the flour does. So, if a change of ½ oz. of sugar cannot be detected, then why attempt to lock down the amount of sugar to within ¼ oz. when ±1 oz will do? So, only lock down the variables as much as you need to – not necessarily as much as you possibly can.
Budget Crunch: Will you have enough money to pay all your bills each month and still can take on that new mortgage payment?
You may have wondered why Metrologist’s refer to the method in which they calculate measurement uncertainty as an uncertainty budget. It is much like your financial budget at home (or at work) where you create a list of all the items that eat away at your income (revenue). Having a list, or budget, allows you to see everything that impacts you financially (financial uncertainty components) all in one place. Some of these costs are fixed (like your car payment or your rent/mortgage payment) and some change every month (like the amount you spend on gas for your car, groceries, eating at restaurants, etc.). If you have more costs than you have take-home pay, then you must adjust keep your budget balanced. So, you usually look at the items that are costing you the most and find ways to reduce or eliminate them because focusing on the small items don't have as much of an impact (i.e., don’t sweat the small stuff). It’s the same with an uncertainty budget: you make a list of all the variables (measurement uncertainty components) that might cause the true measurement value to change and then estimate how large these variables might be. Once you’ve made sure everything has been considered, you combine these variables to understand how big the total window of uncertainty really is. This total uncertainty surrounds the expected measurement value (nominal measurement) to indicate how much that measurement value could possibly vary. If the combined uncertainty is too large (i.e., causes too much variance in the measurement), then you might try to reduce the largest components which will have the biggest impact on the result.
Travel Uncertainty:
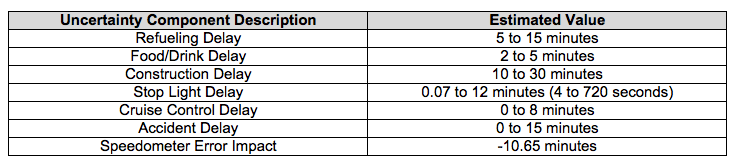
Let’s look at a detailed example, using the travel example. The things you know for certain are the distance between your origination and destination points and the fact that your GPS indicates that the trip should take 4 hours and 38 minutes to complete. Things that you know will cause variance include stopping for gas and food, road construction, the amount of time spent at stop lights/signs, your ability to maintain a constant speed through each segment of the trip, accidents, the accuracy of your speedometer, and your tire size. If these variables, or travel time uncertainty components, were all negligible then the trip would take 4 hours and 38 minutes (assuming the GPS has accounted for the speed limits on each segment of the trip). But the probability is very low that you will always maintain the maximum speed allowed and never stop from point A to point B.
Now that we’ve listed all the variables (are there any others?) we need to estimate values for each of them. How many times will you stop for gas? To determine this, it would be good to know the gas mileage of the vehicle you will be driving. Let’s say you know that you’ve historically could get 20 miles per gallon. You also know that your gas tank is 16 gallons. Multiplying these two figures tells you that you can drive 320 miles before you will run out of gas. The implication here is that you do not need to stop for gas; that is, if you don’t run into anything that might eat up that extra 20 miles of fuel. So, to be on the safe side, you plan to stop for gas once during the trip. From experience, you know that you have never refueled your tank any faster than 5 minutes and that it has never taken longer than 15 minutes. You’ll also grab a drink when you stop, which will take an extra 2 to 5 minutes. We’ll come back to these estimates once we’ve made estimates for the other variables (uncertainty components).
Next, because it is summertime and with that comes a guarantee of highway construction, you estimate that this will cause anywhere from 10 to 30 minutes of delay.
As for stop lights and stop signs, you know from taking this trip previously that there are 3 stop lights in your town before getting on the highway and 5 stop lights in the town you are going to before arriving at your destination. The amount of time you spend sitting at a red light depends on a few factors: sensors in the road for opposing traffic, a maximum amount of time the light will remain on red, and the time at which you pull up to the red light. You estimate that half of these lights will be on green as you pass through them and that you must stop for some period at the others. The maximum time for a red light is 180 seconds. So, you will wait as short as 1 second per light and if 180 seconds per light.
You plan to minimize the variation in your speed by using your cruise control, but you’ve learned all too well that you’re bound to get behind an eighteen-wheeler passing another big truck, which means you’ll have to hit the brake a few times. You estimate that this break in cruise control will happen 4 times during the trip, causing you to lose up to two minutes each time.
While you’d be lucky not to experience bumper-to-bumper traffic due to an accident, you decide to plan on at least one and estimate that this will cause up to a 15-minute delay.
Your speedometer has some amount of inaccuracy. Your tire size also affects the accuracy of your speedometer. To determine this combined effect, you drive along a stretch of highway, maintaining the speed at 65 mph while a friend measures the time lapse on a stopwatch. When you pass a mile marker, you say ‘Start’ and your friend starts the stopwatch. When you pass another mile marker 5 miles down the road, you say ‘Stop’ and your friend stops the stopwatch. When you return home, you convert the time lapse (in minutes and seconds) to hours: the stopwatch read 4:24:71, or 4 minutes and 24.7 seconds. This converts to 0.074 hours. You divide the 5-mile distance traveled by 0.074 hours to determine that you were traveling at a speed of 67.6 mph when your speedometer read 65 mph. You could do this at different speeds to determine whether you have the same error across the speedometer, but to simplify things (yeah, right) you decide to use this error of +2.6 mph in your total uncertainty, regardless of the speed you will be going in each segment of the trip. This error shaves off about 11 minutes from the trip.
Now that we’ve evaluated all the uncertainty components related to our travel time, let’s review these and put them into a travel time uncertainty budget.